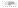


NNs are structures, inspired from the corresponding
biological neural systems, that consist of interconnected processing units
(called neurons) arranged in a distinct layered
topology. In analogy to the biological neural structures, the function of the
network is determined from the connections between the units. Topology and
connections determine the architecture of a network.
Static Feedforward Neural Networks (NNs), with strictly
forward connections, often have one or more intermediate hidden layers of nonlinear processing units, followed by an output layer of linear units. Such an architecture may be summarized in
the notation:
where I is the number of inputs, Hi is the number of neurons in the ith hidden layer, O is the number of units in the
output layer and C is the total number of connections (known as synaptic
weights or just weights) and biases.
The connection from neuron i to neuron j is characterized
by a real number weight wij. The
output ai of neuron i is transmitted through this
connection to neuron j and multiplies its strength by the weight wij, forming accordingly the weighted
input wijai. Each neuron has additionally a bias
b which is summed with its weighted inputs to form its net input. This
quantity feeds the activation
function f that produce the output aj of neuron j.
Given two set of data, input/output pairs, NNs are able to learn a specific nonlinear mapping by adjusting the network
weights and bias by using the training algorithm (see Machine Learning Procedure). The goal of network training is
not to learn an exact representation of the known halflives itself, but rather
to build a statistical model of the process which generates the half-lives.
This is very important for a good generalization and
leads to a reliable statistical model. The mostly used training algorithm is the back-propagation
(BP) algorithm in many
variations, where a steepest descent
gradient approach and a chain-rule are adopted for back-propagating the error
correction from the output layer. The initial values of the free parameters (weights and biases) play also a crucial role in the final
result. After a large number of computer experiments, we reach a model suitable to both approximate the observed â- decay
half-life systematics and to generalize well to unknown regions. The main
features of our model are recapitulated in the table below.


N. J. Costiris(1), E. Mavrommatis (1), K. A. Gernoth (2) and J. W. Clark (3)
(1) Physics Department, Division of
Nuclear and Particle Physics, University of Athens, GR-15771 Athens,
Greece
(2) Department of Physics, UMIST, P.O.
Box 88, Manchester M60 1QD, United
Kingdom
(3) McDonnell Center for the Space
Sciences and Department of Physics, Washington University, St. Louis, Missouri
63130, USA
Statistical modeling of nuclear data
provides a novel approach to nuclear systematics which
valuably complements the phenomenological and semi-microscopic theories.
Currently, there is an urgent need for reliable estimates of â- decay halflives of
nuclei far from stability. This need is driven
both by the experimental programs of existing and future radioactive ion-beam
facilities and by ongoing major efforts in astrophysics toward understanding
supernova explosions, and the processes of nucleosynthesis in stars, notably
the r-process. In this work, the beta decay halflives
problem is dealt as a many-body system optimization problem, which is resolved
in the statistical framework of machine learning. Continuing past similar
approaches, we deploy a more sophisticated Artificial Neural Networks (NNs) statistical methodology to global
model the halflives systematics of nuclei that decay 100% by the â- mode in their ground states. A fully
connected, static, multilayered feedforward neural network NN was adopted and trained using the Levenberg-Marquardt
optimization algorithm with a
combination of two well-established techniques for improving generalization,
namely, Bayesian
regularization and cross-validation. We report here our methodology for the
arising large-scale calculations and discuss and compare our
results with the available experimental [7], the theoretical ones and some
other results obtained with analogous techniques (previous ANNs and more
recent Support
Vector Machines (SVMs)
approaches). We then give predictions
for nuclei that are far from the stability line and focus in particularly to
those involved in the r-process
nucleosynthesis. It seems that
our new statistical “theory-thin” data-driven global model can at least match or even
surpass the predictive performance of the best conventional “theory-thick” theory-driven global models.

Introduction

Main â-Decay
Global Models

Machine Learning Procedure

Results













Several models for determining â- halflives have
been proposed and applied during the last few decades. These include the more
phenomenological models based on Gross Theory (GT) [1], as
well as models (in various versions)
that employ the Quasiparticle
Random-Phase Approximation (QRPA) [2,4],
along with some approaches based on shell-model
calculations. The latest version of the RPA models developed by Möller
and coworkers, combines the pn-QRPA
model with the statistical Gross Theory of
ff-decay [3,11]. There are also
some models in which the ground state of the parent nucleus is described by
the extended
Thomas-Fermi plus Strutinsky integral method or the Harrtre-Fock BCS and which the use the continuum QRPA (CQRPA) [5]. Recently a relativistic
pn-QRPA (RQRPA) model has been applied in the treatment of
neutron-rich nuclei in the N = 50 and 82 regions [6].


Machine
learning statistical framework
target
(Log10Tâ,exp)
Output
(Log10Tâ,calc)
input
[Z,N,ä]
Machine:
Neural
Network
with C weights
weights
adjustment
comparison





Objective: The
minimization of the cost function ED
The Levenberg - Marquardt update rule (LM algorithm)
where w represents the vector of weights, J is the Jacobian matrix that contains
first derivatives of the machine errors with respect to the weights, I is the unit matrix, ì is an adjustable parameter that controls the step size and e is a vector of network errors. The
central idea of learning machines is that the free parameters (weights) can be
adjusted by minimizing the cost function (ED ) through a proper training algorithm (LM for example), so that the
machine responds to a desired behavior.
Data Sets
Our â- Decay Global Model [8]

Comparison
With Theory Thick Global Models

Comparison With Experiment


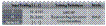
The partitioning of NuSet-B with a cutoff at 106 sec
into the three subsets: Learning,
Validation and Test Sets
NuSet-B
consists of 838 nuclides: 503 (~60\%) of them have been uniformly
chosen to train the network (learning set),
167 (~ 20\%)
to validate the learning
procedure (validation
set) and the remaining 168 (~ 20\%) to evaluate the accu-racy of the prediction (test set). With the exclusion of the long-lived examples
(>106s), one is dealing with a
smaller but more homogeneous collection of nucli-des that facilitates the
training of the network. From now on we will refer to the whole set of 838
nuclides with the term Overall
Mode and to the test set of 168 nuclides (that tests the
extrapability of the model) with the term Prediction Mode.




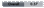



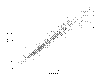
The above Fig. illustrates present
calculations of â-decay
half-lives in comparison with experimental values for nuclides in the learning,
validation and test sets.
Theory
Thick
Global
Models
[1-6]


数はすべての事の中である
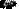
p1
a
p2
pR
b
w1...R







Hidden layers
neuron
A Different Training
Procedure [10]


Previous NN Model
[16-10-1 | 181] [9]
Our NN Model
[3-5-5-5-5-1|116] [8]